Steepest Descent and Conjugate Gradients methods

About

In this project, the Steepest Descent and Conjugate Gradients methods were implemented for solving the following linear systems:

• A₁x = b₁
• A₂x = b₂

where A₁, A₂ ∈ ℝ^n,n and b₁, b₂ ∈ ℝⁿ:

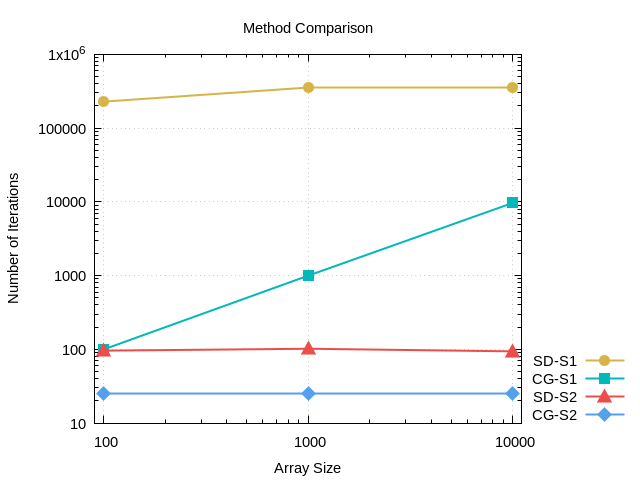
In the context of this exercise, double-precision floating-point arithmetic was used in order to compare the two linear systems in terms of convergence speed and the number of iterations required, as n takes value in {100, 1000, 10000}. Moreover, provided that r^(k) is the residual vector at the k-th step, the maximum residual should be ||r^(k)|| ≤ 0.5 * 10^-4.

The purpose of this project was also to achieve the minimum time complexity for this specific form of input matrices A₁, A₂, b₁ and b₂, taking into account that A₁ and A₂ are pentadiagonal matrices.

Implementation details

The project was implemented in C language.

The C language version supports:

• single and double-precision floating-point arithmetic by typedefing each time fptype to double or float
• optimal and non-optimal versions by defining or not preprocessor macro OPTIMIZED (see Makefile).

Results - Method Comparison